Aurora blog

バイオインフォ・バイオテクノロジーにまつわる情報

遺伝子シグネチャースコアの計算手法

Bioinfo Omics

トランスクリプトームデータを使ったシグネチャースコアの計算手法についてメモを残す。

ssGSEA

Single sample GSEA (ssGSEA) は2009年の論文で最初に使われた手法。由来となるアルゴリズム (GSEA) 自体はそれよりも以前に発表されている。発現量で遺伝子をソートし、任意の遺伝子セット (e.g., パスウェイ) が上位 or 下位に統計的有意にエンリッチしているかを調べる方法。具体的には以下のようなアルゴリズムで計算する。

  1. 全遺伝子を発現量 (または他の指標) で降順 L = {r_{1}, r_{2}, ..., r_{N}} にソート
  2. 遺伝子セット S ごとに以下のスコア ESを計算
    • ES(G, S) = \sum_{i=1}^{\hat{N}} [P_{G}^{w}(G, S, i) - P_{N_{G}}(G, S, i)]
    • P_{G}^{w}(G, S, i) = \sum_{r_{j} \in G, j \leq i} \frac{ |r_{j}|^{\alpha} }{ \sum_{r_{j} \in G} |r_{j}|^{\alpha} }
    • P_{N_{G}}(G, S, i) = \sum_{r_{j} \notin G, j \leq i} \frac{ 1 }{ (N - N_{G}) }
      • \alpha = 0.25がデフォルトでは設定される
      • r_{j} = j: ランク
  3. 2を \hat{N} = 1から Nまで繰り返す中で ES(G, S)の最大値をスコアとする

doi.org

GSVA

GSVAは2013年の論文で提案された手法。単純な発現量で遺伝子をソートするssGSEAとは異なり、遺伝子ごとに以下のような補正を行った後にソートする。全体的に発現量が高い・低い遺伝子が存在することで生じうるバイアスを防ぐことができる。

  1. 遺伝子 i ごとに以下の補正を行う。発現量が正規分布 (e.g., マイクロアレイ) の場合と、カウントデータの場合で異なるカーネルを使う。
    • x_{ij}: サンプル jにおける遺伝子 iの発現量
    • 正規分布： \hat{F}_{h_{i}} (x_{ij}) = \frac{1}{n} \sum_{k=1}^{n} \int_{-\infty}^{\frac{x_{ij} - x_{ik}}{h_{i}}} \frac{1}{\sqrt{2\pi}} e^{\frac{-t^{2}}{2}} dt
    • カウントデータ： \hat{F}_{r} (x_{ij}) = \frac{1}{n} \sum_{k=1}^{n} \sum_{y=0}^{x_{ij}} \frac{e^{-(x_{ik}+r)} (x_{ik}+r)^{y}}{y!}
      • \sum_{y=0}^{x_{ij}} \frac{e^{-(x_{ik}+r)} (x_{ik}+r)^{y}}{y!}: Poisson(x_{ik}+r)の累積分布関数
      • r: ハイパーパラメータ (Default: 0.5) ( x_{ik}=0だと問題が生じるので)
  2. 補正後のスコアを使って遺伝子をソート
  3. ランキングを以下のようにゼロ周辺に正規化
    • r_{ij} = |p/2 - z_{ij}|
    • p: 遺伝子数
    • z_{ij}: サンプル jにおける遺伝子 iのランク
  4. 遺伝子セット \gamma_{k} ごとに以下のスコアを計算
    • v_{jk}(l) = \frac { \sum_{i=1}^{l} |r_{ij}|^{\tau} I(g(i) \in \gamma_{k}) } { \sum_{i=1}^{p} |r_{ij}|^{\tau} I(g(i) \in \gamma_{k}) } - \frac { \sum_{i=1}^{l} I(g(i) \notin \gamma_{k}) } {p - |\gamma_{k}|}
    • I(g(i) \in \gamma_{k}): 遺伝子 iが遺伝子セット \gamma_{k}に含まれていれば1
    • \tau: ハイパーパラメータ (Default: 1)
  5. v_{jk}の最大値をエンリッチメントスコアとする
    • ES_{jk}^{max} = argmax_{l} (v_{jk})

doi.org

Singscore

Singscoreは2018年に提案された手法。

  1. S_{dir, i} = \frac{\sum_{g} R^{g}_{dir, i}}{N_{dir, i}}
    • S_{dir, i}: サンプル iにおけるスコア
    • dir: 正負の方向性、 正・負の方向に動く遺伝子両方を使ってシグネチャーを計算する場合に設定する。特にシグネチャー遺伝子に方向性がなければ dir=upのみ
    • R^{g}_{dir, i}: 遺伝子 gのランキング。 dir=upの場合は昇順、 dir=downの場合は降順
    • N_{dir, i}: シグネチャー遺伝子のうち、発現データで計測されている遺伝子の数
  2. \overline{S}_{dir, i} = \frac{S_{dir, i} - S_{min, i}}{S_{max, i} - S_{min, i}}
    • \overline{S}_{dir, i}: サンプル iにおける正規化スコア
    • S_{min, i} = \frac{N_{dir, i} + 1}{2}: 取りうる最小のスコア S
    • S_{max, i} = \frac{2N_{total, i} - N_{dir, i} + 1}{2}: 取りうる最大のスコア S
      • N_{total, i}: サンプル iで計測されている遺伝子の数
  3. ( dirが正負両方ある場合) \overline{S}_{total, i} = \overline{S}_{up, i} + \overline{S}_{down, i}

bmcbioinformatics.biomedcentral.com

いまいちどedgeRの理論を理解する

Bioinfo Omics

edgeR

RNA-seqの発現変動遺伝子 (DEG) 解析のためのRパッケージであるedgeRは、DEseq2とともに広く使われており、デファクトスタンダードともいえる扱いになっている。edgeRの統計的な理論やアルゴリズムを説明した日本語の文章があまり見つからなかったので、このブログに備忘録として記載しておく。以下の文章・文献を参考にした。

DGEListクラス

edgeRでは遺伝子発現データとメタデータ (e.g., group等の情報) をDGEListというクラスで扱う。後述の通りedgeRはリードカウント値をインプットに用いるため、FPKMやTPMなどの正規化後の数値を使わないように注意。ここでは便宜的に以下のコードでテストデータを作った。

example("DGEList")
y = DGEList(Counts, group=c(1,1,2,2))

低発現遺伝子の除去：filterByExpr

edgeRのマニュアルに従うとfilterByExpr関数を使い低発現遺伝子を除外する。関数の説明を見てもいまいち理解できないので関数の中身を見てみた。filterByExpr.defaultとタイプすると関数の中身が見えた。2016年の論文で採用されている前処理方法を実装しているようだが、あまり直感的な方法ではないので、別のシンプルな方法が好みであれば、そちらを使っても良いと思う。

  1. 一番小さいグループのサンプル数MinSampleSizeを求める
  2. MinSampleSizeがlarge.nより大きい場合は以下のようにMinSampleSizeを更新
    MinSampleSize <- large.n + (MinSampleSize - large.n) * min.prop
  3. 各サンプルのsize factor lib.sizeを計算 (デフォルトではlib.sizeは合計リード数)
  4. lib.sizeの中央値MedianLibSizeを計算
  5. 発現量の閾値を以下のように計算 (min.countはデフォルトでは10)
    CPM.Cutoff <- min.count/MedianLibSize * 1e+06
  6. 以下の基準を満たさない遺伝子を除外
    • CPM値がCPM.Cutoffを超えているサンプル数がMinSampleSize以上
    • 全サンプル中の合計リード数がmin.total.count (default: 15) 以上
function (y, design = NULL, group = NULL, lib.size = NULL, min.count = 10, min.total.count = 15, large.n = 10, min.prop = 0.7, ...) 
{
    y <- as.matrix(y)
    if (mode(y) != "numeric") 
        stop("y is not a numeric matrix")
    if (is.null(lib.size)) 
        lib.size <- colSums(y)
    if (is.null(group)) {
        if (is.null(design)) {
            message("No group or design set. Assuming all samples belong to one group.")
            MinSampleSize <- ncol(y)
        }
        else {
            h <- hat(design)
            MinSampleSize <- 1/max(h)
        }
    }
    else {
        group <- as.factor(group)
        n <- tabulate(group)
        MinSampleSize <- min(n[n > 0L])
    }
    if (MinSampleSize > large.n) 
        MinSampleSize <- large.n + (MinSampleSize - large.n) * 
            min.prop
    MedianLibSize <- median(lib.size)
    CPM.Cutoff <- min.count/MedianLibSize * 1e+06
    CPM <- cpm(y, lib.size = lib.size)
    tol <- 1e-14
    keep.CPM <- rowSums(CPM >= CPM.Cutoff) >= (MinSampleSize - 
        tol)
    keep.TotalCount <- (rowSums(y) >= min.total.count - tol)
    keep.CPM & keep.TotalCount
}

Scaling factorの計算 calcNormFactors

RNA-seqでは各mRNAの絶対量を推定することが不可能であるため、RPKMやTPMなどの相対値 *1 へと変換することでデータの解釈を行うが、相対値ならではの問題が存在する。例えば、一部の遺伝子が非常に強く発現している場合に、相対値へと変換すると、他の遺伝子の発現量が全体的に過小評価されてしまうことがある。このような相対値を使って群間比較を行えば、誤って大量の遺伝子が変動していると判断される可能性がある *2。

そこでedgeRでは、RPKM/TPMのような単純な合計リード数に基づく補正でなく、TMM (default) やRLE (methodオプションで選択可能) といった方法でScaling factorを求める。TMMは「多くの遺伝子は変動していない」という過程のもとにScaling factorを探す手法である。詳細はbiopapyrus.jpの記事を参照されたい。

  1. 各サンプルの75%ile (上位25%の遺伝子の発現量) を計算 (変数: f75)
  2. f75の値がf75の平均に最も近いサンプルをrefColumnとする。
  3. 各サンプルiとrefColumnの間でTMMによりScaling factor fを求める
calcNormFactors = function (object, 
          lib.size = NULL, 
          method = c("TMM", "TMMwsp", "RLE", "upperquartile", "none"), 
          refColumn = NULL,
          logratioTrim = 0.3, 
          sumTrim = 0.05, 
          doWeighting = TRUE, 
          Acutoff = -1e+10, 
          p = 0.75, 
    ...) 
{
    x <- as.matrix(object)
    if (any(is.na(x))) stop("NA counts not permitted")
    nsamples <- ncol(x)
    if (is.null(lib.size)) {
        lib.size <- colSums(x)
    }
    else {
        if (anyNA(lib.size)) 
            stop("NA lib.sizes not permitted")
        if (length(lib.size) != nsamples) {
            if (length(lib.size) > 1L) 
                warning("calcNormFactors: length(lib.size) doesn't match number of samples", call. = FALSE)
            lib.size <- rep_len(lib.size, nsamples)
        }
    }

    method <- match.arg(method)
    allzero <- .rowSums(x > 0, nrow(x), nsamples) == 0L
    if (any(allzero)) x <- x[!allzero, , drop = FALSE]
    if (nrow(x) == 0 || nsamples == 1) method = "none"
    f <- switch(method, TMM = {
        if (is.null(refColumn)) {
            f75 <- suppressWarnings(.calcFactorQuantile(data = x, lib.size = lib.size, p = 0.75))
            if (median(f75) < 1e-20) {
                refColumn <- which.max(colSums(sqrt(x)))
            } else {
                refColumn <- which.min(abs(f75 - mean(f75)))
            }
        }
        f <- rep_len(NA_real_, nsamples)
        for (i in 1:nsamples) f[i] <- .calcFactorTMM(obs = x[, i], ref = x[, refColumn], libsize.obs = lib.size[i], 
            libsize.ref = lib.size[refColumn], logratioTrim = logratioTrim, 
            sumTrim = sumTrim, doWeighting = doWeighting, Acutoff = Acutoff)
        f
    }, 
    # TMMwsp = {}, # 割愛
    # RLE = {} # 割愛
    )
    f <- f/exp(mean(log(f)))
    names(f) <- colnames(x)
    f
}

.calcFactorQuantile <- function (data, lib.size, p=0.75){
    f <- rep_len(1,ncol(data))
    for (j in seq_len(ncol(data))) f[j] <- quantile(data[,j], probs=p)
    if(min(f)==0) warning("One or more quantiles are zero")
    f / lib.size
}

# サンプルobsのScaling factorをrefに対してTMMにより計算
.calcFactorTMM <- function(obs, ref, libsize.obs=NULL, libsize.ref=NULL, logratioTrim=.3, sumTrim=0.05, doWeighting=TRUE, Acutoff=-1e10)
{
    obs <- as.numeric(obs)
    ref <- as.numeric(ref)

    if( is.null(libsize.obs) ) nO <- sum(obs) else nO <- libsize.obs
    if( is.null(libsize.ref) ) nR <- sum(ref) else nR <- libsize.ref

    logR <- log2((obs/nO)/(ref/nR))          # log ratio of expression, accounting for library size
    absE <- (log2(obs/nO) + log2(ref/nR))/2  # absolute expression
    v <- (nO-obs)/nO/obs + (nR-ref)/nR/ref   # estimated asymptotic variance

  # remove infinite values, cutoff based on A
    fin <- is.finite(logR) & is.finite(absE) & (absE > Acutoff)

    logR <- logR[fin]
    absE <- absE[fin]
    v <- v[fin]

    if(max(abs(logR)) < 1e-6) return(1)

#   taken from the original mean() function
    n <- length(logR)
    loL <- floor(n * logratioTrim) + 1
    hiL <- n + 1 - loL
    loS <- floor(n * sumTrim) + 1
    hiS <- n + 1 - loS

#   keep <- (rank(logR) %in% loL:hiL) & (rank(absE) %in% loS:hiS)
#   a fix from leonardo ivan almonacid cardenas, since rank() can return
#   non-integer values when there are a lot of ties
    keep <- (rank(logR)>=loL & rank(logR)<=hiL) & (rank(absE)>=loS & rank(absE)<=hiS)

    if(doWeighting)
        f <- sum(logR[keep]/v[keep], na.rm=TRUE) / sum(1/v[keep], na.rm=TRUE)
    else
        f <- mean(logR[keep], na.rm=TRUE)

#   Results will be missing if the two libraries share no features with positive counts
#   In this case, return unity
    if(is.na(f)) f <- 0
    2^f
}

2群間比較

edgeRでは2群間比較のための検定手法が3つ (exactTest, glmLRT, glmQLFTest) 用意されている。開発者によると *3 glmQLFTestが最も推奨される手法であるとのこと。

負の二項分布 (Negative binomial distribution) について

カウントデータのモデリングによく用いられるポアソン分布でサンプル iの遺伝子 gのリードカウント y_{ig}をモデル化すると以下のようになる。 N_{i}はサンプル iの合計リード数で、 \pi_{ig}はサンプル iにおける遺伝子 gの割合を表す。

y_{ig} \sim Poisson(N_{i} \pi_{ig})

上記のモデルは合計リード数 N_{i}のうち、割合 \pi_{ig}で発言する遺伝子 gに由来するリード数の分布を表す *4。しかし実際には、サンプル iのデータを複数回 (biological replicatesを) 取得した場合には、施行回ごとに割合 \pi_{ig} には生物的なゆらぎが生じるはずであり、ポアソン分布ではこの生物的ゆらぎ *5 を考慮できていないと言える。*6

このような場面で使われるのが負の二項分布 (Negative binomial distribution) である。負の二項分布は、ポアソン分布のパラメータ \lambdaが、ガンマ分布 \lambda \sim Gamma(r, \frac{p}{1-p}) に従うと仮定した分布である。edgeRやDEseq2などのRNA-seqのDEG解析でデファクトスタンダードとされている手法は負の二項分布でリードカウントデータをモデリングしている。次の式展開はこのページ等を参照されたい。以下の分布は、確率 pで成功するイベントを r回発生させるまでに x回失敗する確率、を表しているといえる。

{
\begin{align}
NB(x |r, p) &= \int_{0}^{\infty} Poisson(x|\lambda) Gamma(r, \frac{p}{1-p}) d\lambda  \tag{1} \\\
&= {}_{x+r-1} \mathrm{C}_{x} (1-p)^{r} p^{x} 
\end{align}
}

平均と分散は以下のようになる。

  • E(x) = r \frac{1-p}{p}
  • Var(x) = r \frac{1-p}{p^{2}}

また、負の二項分布は次の形式で表されることもある。このあたりはこのスライド にロジックが説明されているが、 \phi = r、 p = \frac{\phi}{\phi + \mu}とすると以下のように表すことができる。この場合は、 r回成功させるまでに平均 \mu回失敗するイベントを、 r回発生させるまでに x回失敗する確率、を表していると解釈することができる。

{
\begin{align}
NB(x |\mu, \phi) &= \int_{0}^{\infty} Poisson(x|\lambda) Gamma(\phi, \frac{\phi}{\mu}) d\lambda \tag{2} \\\
&= {}_{x+\phi-1} \mathrm{C}_{x} (\frac{\mu}{\phi + \mu})^{\phi} (\frac{\phi}{\phi + \mu})^{x} 
\end{align}
}

平均と分散は以下のようになる。

  • E(x) = \mu
  • Var(x) = \mu + \mu^{2} / \phi

Stanでは以上の２つの形式で負の二項分布を利用することができるようになっている (NegBinomial, NegBinomial2)。一方で、PyroやTensorflow probabilityでは前者の形式でしか負の二項分布が提供されていない。また、後述の通りedgeRではパラメータの定義がまた若干異なるので注意。

edgeRでは負の二項分布のパラメータを前述の２つの形式とは異なる形で定義している *7。edgeRでDispersion parameterと呼ばれるパラメータ \phiは、式(2)の \phiの逆数である。

{
\begin{align}
NB(x |\mu, \phi) &= \int_{0}^{\infty} Poisson(x|\lambda) Gamma(\phi, \frac{1}{\phi\mu}) d\lambda \tag{2} \\\
&= {}_{x+\phi^{-1}-1} \mathrm{C}_{x} (\frac{\phi\mu}{1 + \phi\mu})^{1/\phi} (\frac{1}{1+ \phi\mu})^{x} 
\end{align}
}

この場合は分散は以下のようになる。 \phi = 0のときポアソン分布の分散 Var(x) = \muと等しくなることから、Dispersion parameter \phiは、生物的ゆらぎの大きさを表すパラメータとみなすことができる。

  • Var(x) = \mu + \mu^{2} \phi

estimateDisp

exactTest

本手法は2007年に出版されたedgeRのオリジナル論文で紹介されている。

doi.org

*1:transcript counts per "Million"

*2:とはいえ、それが生物学的に正しい可能性もあるので、ケースバイケースではあると思う

*3:https://www.youtube.com/watch?v=hQqIBlO_j3o&t=1337s

*4:edgeRのマニュアルではTechnical variationと呼んでいる

*5:edgeRのマニュアルではBiological variationと呼んでいる

*6:また、これが原因で生物学のカウントデータはポアソン分布で仮定されるよりも分散が大きいことが多い。過分散 over-dispersionという表現でよく出てくる。

*7:https://doi.org/10.1093/bioinformatics/btm453

Knowledge graph①： Neo4j Graph Academy備忘録

Graph database

背景

グラフデータベースNeo4jに触る機会がありNeo4j Graph Academyを受講した。忘れそうなポイントをこのページにメモとして残す。

Cypher

MATCH/OPTIONAL MATCH

  • OPTIONAL MATCH: 該当のクエリが存在する場合にのみ結果を返す (存在しない場合はnullを返す)
MATCH (m:Movie) WHERE m.title = "Kiss Me Deadly"
MATCH (m)-[:IN_GENRE]->(g:Genre)<-[:IN_GENRE]-(rec:Movie)
OPTIONAL MATCH (m)<-[:ACTED_IN]-(a:Actor)-[:ACTED_IN]->(rec)
RETURN rec.title, a.name

特定のプロパティのみを持つノードを返す場合

MATCH (m:Movie)
WHERE m.title CONTAINS 'Matrix'
RETURN m { .title, .released } AS movie

MERGE/DELETE

新しいノード・エッジを作成/削除する。以下の性質があるので注意。

  • MERGEは条件に該当するノード・エッジが既に存在する場合は実行されない。
  • MERGEはエッジの方向性を指定しないと「左側のノードから右側のノード」という方向性がデフォルトでアサインされる *1
  • DETACH DELETE: DELETEではエッジを持つノードを削除できない様になっている。こういったノードを削除する場合に使う。
// 以下の様に実行すると全てのノード・エッジが消える (=グラフが完全消去される)
MATCH (n)
DETACH DELETE n

WHERE

以下の演算子が存在

  • =: Equal
  • <>: Not equal
  • >/<: Greater / Less than
  • OR: OR演算子
  • A STARTS WITH B: 文字列AがBで始まっているか
  • A ENDS WITH B: 文字列AがBで終わっているか
  • A CONTAINS B: 文字列AにBが含まれているか

プロパティが存在している場合は以下のように検証可能

MATCH (p:Person)
WHERE p.died IS NOT NULL

SET系

MERGE/MATCHで指定したノード・エッジのプロパティを追加する

  • SET: 常に実行される
  • ON CREATE SET: MERGEによってノード・エッジが作られた時にのみ実行される
  • ON MATCH SET: MERGE実行時に既にノード・エッジが存在する場合にのみ実行される
// Find or create a person with this name
MERGE (p:Person {name: 'McKenna Grace'})

// Only set the `createdAt` property if the node is created during this query
ON CREATE SET p.createdAt = datetime()

// Only set the `updatedAt` property if the node was created previously
ON MATCH SET p.updatedAt = datetime()

// Set the `born` property regardless
SET p.born = 2006

RETURN p

SETではプロパティを追加するだけでなくノードにラベル (Node Type) を追加する場合にも使える

MATCH (p:Person)
WHERE exists ((p)-[:DIRECTED]-())
SET p:Director

プロパティを消す場合にも使える

MATCH (m:Movie)
SET m.genres = null

WITH

WITHを使うことでMATCHの前に特定の値で変数を定義することができる

WITH 'Tom Hanks' AS actorName
MATCH (p:Person)-[:ACTED_IN]->(m:Movie)
WHERE p.name = actorName
RETURN m.title AS movies

WITHを挟むとRETURN文に記載できる変数名がリセットされる。以下のケースのようにRETURNで返したい変数 (e.g., p, m) がある場合はWITHに入れる必要がある。

WITH  'Clint Eastwood' AS a, 'high' AS t
MATCH (p:Person)-[:ACTED_IN]->(m:Movie)
WITH p, m, toLower(m.title) AS movieTitle
WHERE p.name = a
AND movieTitle CONTAINS t
RETURN p.name AS actor, m.title AS movie

WITHを使った事例： 平均スコアの計算

MATCH (:Movie {title: 'Toy Story'})-[:IN_GENRE]->(g:Genre)<-[:IN_GENRE]-(m)
WHERE m.imdbRating IS NOT NULL
WITH g.name AS genre,
count(m) AS moviesInCommon,
sum(m.imdbRating) AS total
RETURN genre, moviesInCommon,
total/moviesInCommon AS score
ORDER By score DESC

UNWIND

プロパティのリストに含まれる項目ごとに操作を実行することができる。モデルをリファクタリングする際に使用する事例が紹介されていた。

MATCH (m:Movie)
UNWIND m.genres AS genre
MERGE (g:Genre {name: genre})
MERGE (m)-[:IN_GENRE]->(g)
SET m.genres = null

CREATE CONSTRAINT

特定のプロパティ (e.g., ID) に重複を許さないなどの制約を設けることができる。検索の速度改善にもつながるらしい。

CREATE CONSTRAINT Genre_name IF NOT EXISTS
FOR (x:Genre)
REQUIRE x.name IS UNIQUE

ORDER BY

結果を何らかのプロパティでソートする場合に使う

  • DESC: 降順
MATCH (p:Person)
WHERE p.born IS NOT NULL
RETURN p.name AS name, p.born AS birthDate
ORDER BY p.born DESC

２つ以上の条件を使う場合

MATCH (m:Movie)<-[ACTED_IN]-(p:Person)
WHERE m.imdbRating IS NOT NULL
RETURN m.title, m.imdbRating, p.name, p.born
ORDER BY m.imdbRating DESC, p.born DESC

CASE-WHEN

MATCH (m:Movie)<-[:ACTED_IN]-(p:Person)
WHERE p.name = 'Henry Fonda'
RETURN m.title AS movie,
CASE
WHEN m.year < 1940 THEN 'oldies'
WHEN 1940 <= m.year < 1950 THEN 'forties'
WHEN 1950 <= m.year < 1960 THEN 'fifties'
WHEN 1960 <= m.year < 1970 THEN 'sixties'
WHEN 1970 <= m.year < 1980 THEN 'seventies'
WHEN 1980 <= m.year < 1990 THEN 'eighties'
WHEN 1990 <= m.year < 2000 THEN 'nineties'
ELSE  'two-thousands'
END
AS timeFrame

UNWIND

リストを分解、行へと分ける

MATCH (m:Movie)-[:ACTED_IN]-(a:Actor)
WHERE a.name = 'Tom Hanks'
UNWIND m.languages AS lang
RETURN m.title AS movie,
m.languages AS languages,
lang AS language

CALL

サブクエリをつくる。例えば下記のように実行すればMovieのRatingについての検索範囲を絞る (=効率を上げる) ことが可能。

CALL {
   MATCH (m:Movie) WHERE m.year = 2000
   RETURN m ORDER BY m.imdbRating DESC LIMIT 10
}
MATCH  (:User)-[r:RATED]->(m)
RETURN m.title, avg(r.rating)

以下のように途中にサブクエリを挟むことも可能

MATCH (m:Movie)
CALL {
    WITH m
    MATCH (m)<-[r:RATED]-(u:User)
     WHERE r.rating = 5
    RETURN count(u) AS numReviews
}
RETURN m.title, numReviews
ORDER BY numReviews DESC

UNION

2つのクエリの出力を連結する。2つのクエリは同じ項目をリターンする必要がある。

  • UNION ALL: ALLをつけないと2つのクエリで重複する行は除外される (DISTINCTと同等)が、つけると重複も結果として出力される
MATCH (m:Movie) WHERE m.year = 2000
RETURN {type:"movies", theMovies: collect(m.title)} AS data
UNION ALL
MATCH (a:Actor) WHERE a.born.year > 2000
RETURN { type:"actors", theActors: collect(DISTINCT a.name)} AS data

Methods

  • exists: 引数のクエリに該当するノード・エッジが存在するかTRUE/FALSEを返す
  • not exists: 引数のクエリに該当するノード・エッジが存在しない場合にTRUEを返す
  • keys: ラベル・リレーションに存在するプロパティの一覧を返す
  • coalesce: 第一引数がnullでなければ第一引数を、nullであれば第二引数を返す
  • split: string型を特定の文字でsplitしてlist型へ変換する
  • toInteger: int型へ変換
  • type: ラベル・リレーションのタイプを返す
  • size: リストのサイズを返す
  • date/datetime/time: 現時刻をdate/datetime/time型で返す
  • shortestPath: 最短経路を返す
  • trim: stringの先頭・末尾にある空白を取り除く

以下の関数はAggregation (group by)する

  • count: 行数をカウントする
  • collect: 該当するノード・エッジが複数ある場合にリストとして返す
  • min/max/stddev/avg/sum: 数値処理
MATCH (p:Person)-[r]->(m:Movie)
WHERE  p.name = 'Tom Hanks'
RETURN m.title AS movie, type(r) AS relationshipType

exists

MATCH (p:Person)
WHERE exists ((p)-[:ACTED_IN]-())
SET p:Actor

split/coalesce

String型のプロパティ (e.g., "A|B") をリスト型 (e.g., ["A", "B"]) へ変換する事例が紹介されていた。

MATCH (m:Movie)
SET m.countries = split(coalesce(m.countries,""), "|"),
m.languages = split(coalesce(m.languages,""), "|"),
m.genres = split(coalesce(m.genres,""), "|")

collect

MATCH (p:Person)-[:ACTED_IN]->(m:Movie)
WHERE p.name ='Tom Cruise'
RETURN collect(m.title) AS tomCruiseMovies, size(collect(m)) AS tomCruiseMovieCount

shortestPath

MATCH p = shortestPath((p1:Person)-[*]-(p2:Person))
WHERE p1.name = "Eminem"
AND p2.name = "Charlton Heston"
RETURN  p
MATCH p = shortestPath((p1:Person)-[:ACTED_IN*]-(p2:Person))
WHERE p1.name = "Eminem"
AND p2.name = "Charlton Heston"
RETURN  p
MATCH (p:Person {name: 'Eminem'})-[:ACTED_IN*1..4]-(others:Person)
RETURN  others.name

APOC系

APOC (Awesome Procedures on Cypher) ライブラリの関数は厳密にはCypherの関数ではないので CALL で呼び出す必要がある

  • apoc.meta.nodeTypeProperties: 各ノードが有するプロパティの情報 (e.g., データ型) を返す
  • apoc.meta.relTypeProperties: 各エッジが有するプロパティの情報 (e.g., データ型) を返す
CALL apoc.meta.nodeTypeProperties()

Parameters

:paramでパラメータを設定、Cypherクエリの中で使うことが可能

// パラメータの設定
:param number: 10
:param actorName: 'Tom Hanks'

// 設定されたパラメータを確認する
:params: 
// :params {} // 全パラメータを削除

MATCH (p:Person)-[:ACTED_IN]->(m:Movie)
WHERE p.name = $actorName
RETURN p, m

JavascriptとかPythonとかで以下のように使える

def get_actors(tx, movieTitle): # (1)
  result = tx.run("""
    MATCH (p:Person)-[:ACTED_IN]->(m:Movie)
    WHERE m.title = $title
    RETURN p
  """, title=movieTitle)

  # Access the `p` value from each record
  return [ record["p"] for record in result ]

with driver.session() as session:
    result = session.read_transaction(get_actors, movieTitle="Toy Story")

Graph modeling

Naming conventions

ラベル・リレーション・プロパティには以下の命名規則を使うことがベストプラクティスとされている。

  • ラベル (Node type)： CamelCase (e.g., Company, HighSchool)
  • リレーション (Edge type)： 大文字 & アンダースコア (e.g., FOLLOWS, MARRIED_TO)
  • プロパティ： camelCase (e.g., deptId, firstName)

Importing CSV

LOAD CSV

  • LOAD CSV
  • WITH HEADERS: ヘッダー行が存在する場合に指定する
  • FIELDTERMINATOR: csvでない場合に使う。区切り文字を指定する。
CALL {
LOAD CSV WITH HEADERS
FROM 'https://data.neo4j.com/importing/2-movieData.csv'
AS row
WITH row WHERE row.Entity = "Join" AND row.Work = "Acting"
MATCH (p:Person {tmdbId: toInteger(row.tmdbId)})
MATCH (m:Movie {movieId: toInteger(row.movieId)})
MERGE (p)-[r:ACTED_IN]->(m)
ON CREATE
SET r.role = row.role
SET p:Actor
}

Neo4j Data Importer

GUIで動かせるツール。ローカル環境にあるCSV形式のデータ (１行目にヘッダが必須) をNeo4jへインポートできる。よくできているがエンジニアが使うかは微妙と感じる。リスト型のプロパティはインポートできないなどプログラムでのデータインポートと比較して制限がある。

*1:Undirected edgeの作り方がよくわからない。同じクエスチョンがGithubでissueとして投稿されている https://github.com/neo4j/neo4j/issues/13009

Pyroでベイズモデリング①：基本の確認

Python Bayesian inference

Pyro

PyroはUberが作った確率的プログラミングのためのPythonライブラリ。PyTorchをベースにしており、PyTorchで実装したニューラルネットを組み込んだ深層生成モデルの開発ができる。最近、シングルセルデータやマルチオミクスデータを対象とした深層生成モデルが多数報告されており、自分でも実装＆既存のモデルをカスタマイズできるようになりたいと考えていたので勉強してみた。Pyroの公式ドキュメントは充実しており、読んでいるだけで面白く勉強になるのだが、試している中で疑問に思ったことが多々あったので、メモを残していこうと思う。

pyro.ai

Stanのような歴史の長い確率的プログラミング言語と比較すると、日本語で書かれている資料は少ない。多くの日本語の情報は「ベイズ線形回帰をPyroで実装してみた」みたいな内容が多いので、このシリーズでは、より複雑なモデルを実装することにトライしていこうと思う。

本記事では以下のページが参考になった。

実装の流れ

Step 1: ModelとGuideの定義

Pyroでは、はじめにModelとGuideを関数として実装する。Modelにはモデルと各パラメータの事前分布を、Guideには変分推論 (後述) で用いる近似事後分布を定義する。

Pyroのチュートリアルで紹介されている線形回帰の事例をもとに実装の流れをさらっていく。この事例では国土の地形の凹凸の多さ(TRI: Terrain Ruggedness Index)とGDPの関係を線形回帰で調べており、アフリカ以外の地域ではTRIが高い (地形の凹凸が高い) ほどGDPが低いのに対して、アフリカではそれと逆の傾向があることを示している。ここでは以下のモデルに対してベイズ推論を行う。変数 Africaはアフリカ地域であれば1が入るバイナリ変数である。

  • log(GDP) \sim \rm{Normal}(\mu, \sigma)
    • \mu = a + b_{A} * Africa + b_{R} * TRI + b_{AR} * Africa * TRI
      • p(a) \sim \rm{Normal}(0, 10)
      • p(b_{A}) \sim \rm{Normal}(0, 1)
    • p(\sigma) \sim \rm{Uniform}(0, 10)

このケースであれば各パラメータの事後分布は解析的に求めることができるが、あえて変分推論で近似事後分布を求める。ここでは変分ベイズでよく用いられる平均場近似 (後述) という近似法を使う。事後分布 p(b_{A}, b_{R}, b_{AR} | X)を近似する、3つの独立した分布 ( q(b_{A}), q(b_{R}), q(b_{AR})) を探索する。以下のコードでは分布 q(b_{A}), q(b_{R}), q(b_{AR})にはそれぞれ正規分布を仮定している。

  • p(b_{A}, b_{R}, b_{AR} | X) \approx q(b_{A}) q(b_{R}) q(b_{AR})

このときModelとGuide (近似事後分布) はPyroで以下のように実装できる。Model/Guideを構成する要素 (Primitives) については後述する。

import torch
from torch.distributions import constraints
import pyro
import pyro.distributions as dist

def model(is_cont_africa, ruggedness, log_gdp):
    a = pyro.sample("a", dist.Normal(0., 10.))
    b_a = pyro.sample("bA", dist.Normal(0., 1.))
    b_r = pyro.sample("bR", dist.Normal(0., 1.))
    b_ar = pyro.sample("bAR", dist.Normal(0., 1.))
    sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
    mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness
    with pyro.plate("data", len(ruggedness)):
        pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)

def guide(is_cont_africa, ruggedness, log_gdp):
    a_loc = pyro.param('a_loc', torch.tensor(0.))
    a_scale = pyro.param('a_scale', torch.tensor(1.), constraint=constraints.positive)
    sigma_loc = pyro.param('sigma_loc', torch.tensor(1.), constraint=constraints.positive)
    weights_loc = pyro.param('weights_loc', torch.randn(3))
    weights_scale = pyro.param('weights_scale', torch.ones(3), constraint=constraints.positive)
    a = pyro.sample("a", dist.Normal(a_loc, a_scale))
    b_a = pyro.sample("bA", dist.Normal(weights_loc[0], weights_scale[0]))
    b_r = pyro.sample("bR", dist.Normal(weights_loc[1], weights_scale[1]))
    b_ar = pyro.sample("bAR", dist.Normal(weights_loc[2], weights_scale[2]))
    sigma = pyro.sample("sigma", dist.Normal(sigma_loc, torch.tensor(0.05)))

変分推論 (Variational inference)

変分推論については多くの書籍・ウェブサイトで説明されているので、言及する必要はないかもしれないが、自分の中で腑に落ちた説明を以下に残しておく。

N個のパラメータ Theta = (\theta_{1},...,\theta_{N}) を含むモデルを考える。複雑なモデルである場合、パラメータの事後分布 p(\Theta|X)は解析的に求めることができないことが多い。*1 このとき変分推論ではパラメータ ( \Theta = (\theta_{1},...,\theta_{N})) の事後分布 p(\Theta|X)を近似する近似事後分布 q(\Theta)を探索する。以下のKLダイバージェンスが最小となる分布 q(\Theta)を探す。

q(\Theta) = \rm{argmin}_{q(\Theta)} \rm{KL} \lbrack q(\Theta) || p(\Theta|X) \rbrack \tag{1}

ここでは平均場近似による近似がよく使われる。平均場近似では各パラメータ \theta_{i}の分布が互いに独立していて、以下が成り立つ条件を仮定する。

q(\Theta) = \Pi_{i} q(\theta_{i}) \tag{2}

式(1)の最適解を探索するには以下の変分下限(ELBO) L \lbrack q(\Theta) \rbrack を最大化する q(\Theta)を探索すれば良い。

L \lbrack q(\Theta) \rbrack = \int q(\Theta) \ln \frac{p(X, \Theta)}{q(\Theta)} d\Theta \tag{3}

この根拠は以下のように説明できる。 p(X)は以下のように変形できる。左辺 \ln p(X)はデータ Xに対して一定の値なので、\rm{L} \lbrack q(\Theta) \rbrackを最大化することは、KLダイバージェンスを最小化することと等しいと考えられる。

{
\begin{align}
\ln p(X) &= \int q(\Theta) \ln p(X) d\Theta \tag{4} \\\
&= \int q(\Theta) \ln \frac{p(X, \Theta)}{p(\Theta|X)} d\Theta \\\
&= \int q(\Theta) \ln \frac{q(\Theta)p(X, \Theta)}{q(\Theta)p(\Theta|X)} d\Theta \\\
&= \int q(\Theta) \ln \frac{p(X, \Theta)}{q(\Theta)} d\Theta - \int q(\Theta) \ln \frac{p(\Theta|X)}{q(\Theta)} d\Theta \\\
&= \rm{L} \lbrack q(\Theta) \rbrack + \rm{KL} \lbrack q(\Theta) || p(\Theta|X) \rbrack
\end{align}
}

Primitives

Pyroでのモデルの構築に使われる基本単位 (Primitivesと呼ばれる) についてまとめる。

pyro.param

  • パラメータを定義する際に用いる関数
  • 引数
    • name: パラメータの名前 (ParamStoreDictでの管理に使われる)
    • init_tensor: 初期値
    • constraint: 制約条件 (e.g. 正値)
  • パラメータはグローバルで管理されParamStoreDictと呼ばれる領域に保存される。*2
    • pyro.get_param_store()でParamStoreDictの内容をdict型で取得できる
    • pyro.clear_param_store()でParamStoreDictの内容を消去できる。学習後のパラメータを消去したい際に用いる。
  • ParamStoreDictのkeyにはpyro.paramの第一引数"name"の情報が使われるので、パラメータを宣言する際は、他のパラメータと同じ"name"を使わないようにしなければならない。
a_loc = pyro.param('a_loc', torch.tensor(0.))
d = pyro.get_param_store()
d["a_loc"]

tensor(0., requires_grad=True)

パラメータは以下の方法でも取得できる。

pyro.param("a_loc").item()

pyro.sample

  • 確率変数を定義する際に用いる関数
  • 引数
    • name: 確率変数の名前。これをもとにModelの分布とGuideの近似分布を対応させる
    • fn: 分布 (pyro.distributionsのクラスが用いられる)
    • obs: 実測値 ELBOの計算に使われる (default: None)
  • 返値
    • obsが空(None)の場合: 分布fnからサンプリングした値を返す
    • obsが空でない場合: obsに指定した値が返される
a = pyro.sample("a", dist.Normal(0., 1.))
a

tensor(0.5161)

pyro.plate

  • 繰り返し(グラフィカルモデルにおけるプレート)を定義する関数
    • e.g. N個の遺伝子の発現量を１つずつ同じ分布でモデル化する場合
    • pyro.plate内部の確率変数は(特定の条件下で)独立とみなされる
      • 例えば以下のコードでは特定のmean/sigmaにおいてobs内の各変数は独立といえる
      • 並列化により計算を高速化できる
  • 引数
    • name: プレートの名前
    • size: 繰り返しのサイズ
    • subsample_size: ミニバッチのサイズ (default: size)
    • dim: plateをどの次元に対応させるか (default: -1)
      • dim=-1の場合はbatch_shape (後述) のうち一番後ろ (後ろから1番目) をPlateに対応させる
mean = pyro.sample("mean", dist.Normal(0., 1.))
sigma = pyro.sample("sigma", dist.Uniform(0., 10.))

with pyro.plate("data", 5) as idx:
    y = pyro.sample("y", dist.Normal(mean, sigma))
y.shape

torch.Size([5])

batch_shapeとevent_shape

pyro.distributionモジュールの分布クラス (e.g. dist.Normal) は、パラメータに複数の値を与えたり、メソッドexpandを使うことで、複数の分布を同時に定義することができる。このとき、メソッドsampleや、上述のpyro.sampleにより、複数の分布からサンプリングされた値をtorch.tensor型のオブジェクトとして取得することができる。例えば、正規分布 (dist.Normal) のパラメータ ( \mu, \sigma) に4つの値を与えてると、4つの正規分布が同時に定義され、各分布からサンプリングされた値をサイズ4のテンソルで取得することができる。

means = torch.tensor([0.0, 1.0, 2.0, 3.0])
sds = torch.tensor([1.0, 1.0, 1.0, 1.0])
d = dist.Normal(means, sds)
x = pyro.sample("x", d)
x

tensor([0.2222, 1.5773, 0.2363, 3.2264])

これに関連する重要な概念として、分布クラスはbatch_shapeとevent_shapeという属性を持つ。batch_shapeは分布の数を表し、event_shapeは各分布から出力される値の次元数を表す。分布クラスからサンプリングされた値の次元は「batch_shape + event_shape」の形になる (event_shapeが末尾の次元に対応する)。

以下の2つのケースは似ているが、異なるbatch_shapeとevent_shapeとなる。①4つの正規分布を作る場合は、batch_shapeが[4]に対して、event_shapeは (=[1])となる。②の4次元正規分布を作る場合は、①と同様に4次元の値を返す分布が作られるが、1つの分布として扱われるため、batch_shapeが、event_shapeが[4]となる。

① 4つの正規分布を作る場合

means = torch.tensor([0.0, 1.0, 2.0, 3.0])
sds = torch.tensor([1.0, 1.0, 1.0, 1.0])
d = dist.Normal(means, sds)
d.batch_shape, d.event_shape, d.sample().shape

(torch.Size([4]), torch.Size([]), torch.Size([4]))

② 1つの4次元正規分布を作る場合

means = torch.tensor([0.0, 1.0, 2.0, 3.0])
sds = torch.eye(4)
d = dist.MultivariateNormal(means, sds)
d.batch_shape, d.event_shape, d.sample().shape

(torch.Size([]), torch.Size([4]), torch.Size([4]))

to_event

分布クラスのメソッドto_eventを使うと、複数の独立した確率分布を、一つの多次元確率分布として扱うことができるようになる。

① 3x4の独立したベルヌーイ分布

d = dist.Bernoulli(0.5 * torch.ones(3,4))
d.batch_shape, d.event_shape, d.sample().shape

(torch.Size([3, 4]), torch.Size([]), torch.Size([3, 4]))

② 3つの独立した4次元ベルヌーイ分布

d = dist.Bernoulli(0.5 * torch.ones(3,4)).to_event(1) # 末尾1次元を非独立として扱う
d.batch_shape, d.event_shape, d.sample().shape

(torch.Size([3]), torch.Size([4]), torch.Size([3, 4]))

pyro.plateの引数dimについて

上述の通りpyro.plateの引数dimはplateがどのbatch_shapeに対応するかを指定するのに使われる。例えば、以下のコードでは、event_shapeが[3, 4]のベルヌーイ分布が5つ (batch_shape=5) 作られる。サンプリングされる値の次元は「batch_shape + event_shape」の形になるので、この場合は[5, 3, 4]次元のテンソルが出力される。

with pyro.plate("a", 5, dim=-1):
    d = pyro.sample("d", dist.Bernoulli(0.5 * torch.ones(3,4)).to_event(2))
d.shape

torch.Size([5, 3, 4])

Step 2: 学習

ModelとGuideを実装したあとはパラメータの推論を行う。Pyroの変分推論では、Adamなどの確率的な最適化アルゴリズムを使って、事後分布にできるだけ近い近似分布を探索する (SVI: Stochasticなvariational inference)。はじめに、pyro.optimモジュールのクラスを使い最適化のアルゴリズム・条件 (e.g. learning rate) を設定し、SVIクラスでModel/Guide・Optimizer・損失関数 (この場合はELBO) を指定する。つづいてsvi.stepでパラメータの更新を行う。svi.stepはModel/Guideの引数となるデータを受け取り、パラメータを更新し、返り値として損失 (ELBO) を出力する。以下の事例では、for文で5000回パラメータの更新を行っている。

from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam

pyro.clear_param_store() # パラメータのリセット

optimizer = Adam({"lr": .05})
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())

num_iters = 5000
for i in range(num_iters):
    elbo = svi.step(is_cont_africa, ruggedness, log_gdp)
    if i % 500 == 0:
        print("Elbo loss: {}".format(elbo))

Step 3: 事後分布の取得

pyro.infer.Predictiveを使うと以下のように事後分布から各パラメータをサンプリングできる。

from pyro.infer import Predictive
params = ["a", "bA", "bR", "bAR"]
pred_model = Predictive(model, guide, num_samples=2000, return_sites=params)
pred_sample = pred_model(is_cont_africa, ruggedness, log_gdp)
pred_sample["a"]

tensor([[9.1086],
        [9.1260],
        [9.1357],
        ...,
        [9.2670],
        [9.0693],
        [9.0717]])

*1:https://ntacoffee.com/variational-inference/

*2:どうしてこのようなデザインになったのだろうか

シングルセル解析⑧： 細胞の運命を確率的に推定する (Plantir, CellRank)

Bioinfo Single-cell Omics

問題設計

CellRankは、Fabian TheisとDana Pe'erのグループから最近報告された、シングルセルデータから細胞が将来的に辿る状態遷移の可能性を確率的に求める手法。「細胞Aは細胞Bよりも細胞Cへと辿り着く可能性が高い」といった推定ができる。

www.nature.com

Plantir

CellRankのアイデアはDana Pe'erのグループから2019年に発表されたPlantirから発展したものだと思われる。Plantirは、細胞の状態遷移にマルコフ性がある (現在の状態のみが次の状態に影響し、過去の状態は影響しない) と仮定し、上記の課題に挑んでいる。手法の概要は以下の通り*1。

  1. Diffusion mapでscRNA-seqデータを次元圧縮
  2. Top nのDiffusion components (DCs) を使いkNN graph G_{E}を求める
  3. 各細胞のPseudo-time \tau (解析者が選んだ起点からのkNN graphにおける最小パス数) を求める
  4. Pseudo-timeをもとに G_{E}を有向グラフ G_{D}に変換する
    • \tau_{i} - \tau_{j} \leq \sigma_{i}の場合は細胞 iから細胞 jへのエッジと考える*2
  5. 解析者が選んだ終点からのEdgeを G_{D}から除外 *3
  6. G_{D}から細胞間の状態遷移確率行列 Pを求める
  7. 状態遷移確率行列 Pを使ったランダムウォーク

結果として下図dのような結果が得られる。例えば、図dのTrajectoryの(2)に位置する細胞は細胞状態A/B/Cのいずれにも同程度分化できるポテンシャルがあるが、(6)の細胞はB/Cにのみ分化する、といったような解釈ができる。

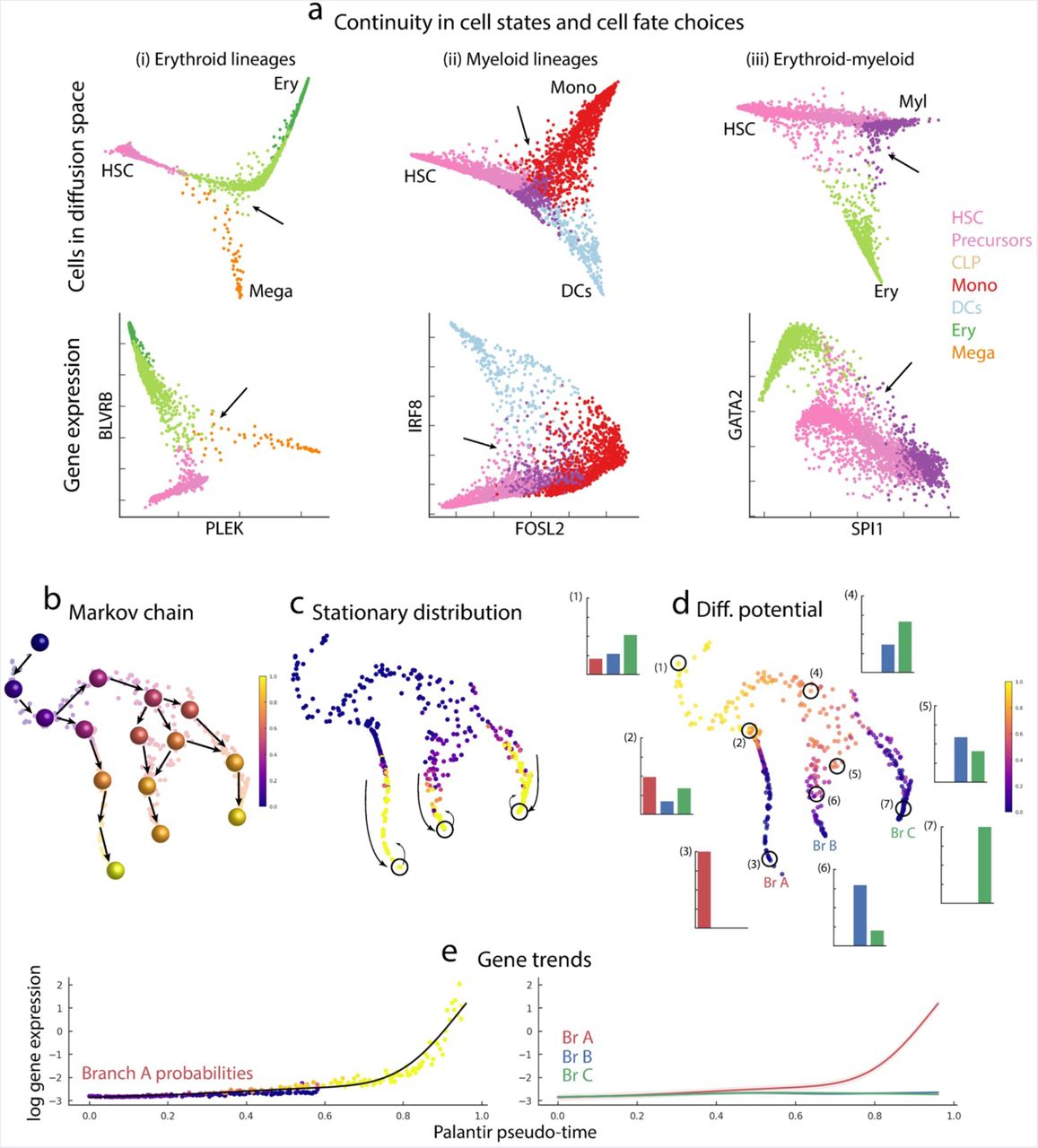
引用元：Setty et al. “Palantir characterizes cell fate continuities in human hematopoiesis” bioRxiv 385328; doi: https://doi.org/10.1101/385328. CC-BY 4.0

www.nature.com

CellRank

CellRankはマルコフ連鎖での細胞状態遷移のモデリングにRNA velocity*4を利用する。RNA velocityを使うことによって、(i) 解析者がTrajectoryの始点・終点を決める必要がなく、(ii) Pseudo-timeに依存したPlantirのように「始点から終点へ」という単一方向の状態遷移を仮定する必要がなくなる。したがって、より複雑な細胞状態遷移の過程を調べるのに適した手法だと言える。RNA velocityに関しては以前の記事を参考のこと。手法の概要は以下の通り。7-8のあたりの展開は正直理解できていない。

  1. kNN graphを作る
    • Plantirと違いDiffusion map以外の次元圧縮法を適用可能 (Default: PCA)
  2. Cell-cell adjacency matrix A \in R^{N \times N}
    • 細胞 iと jがいずれかのkNNに含まれていない場合: A_{ij} = 0
    • それ以外: A_{ij} = \rm{dist}(x_{i}, x_{j})
      • dist: デフォルトはユークリッド距離
      • x_{i}: first top n PCs of cell i (Default: top 30 PCs)
  3. Connectivity kernel P^{s} \in R^{N \times N}
    • P^{s} = row-normalized A
  4. Velocity kernel P^{v} \in R^{N \times N}
    • 下図b参照
    • P^{v}_{ij} = \frac{ \rm{exp} (\sigma c_{ij}) }{ \sum_{k \in K_{i}} \rm{exp} (\sigma c_{ik}) }
      • c_{ij} = \rm{corr} (v_{i}, s_{ij})
        • v_{i}: 細胞 iのVelocity
        • s_{ij} = x_{i} - x_{j}: 細胞 iと jの遺伝子発現の差
      • K_{i}: 細胞 iのkNN
      • \sigma = 1 / \rm{median}_{k \in K_{i}}(c_{ik})
        • VelocityがkNNのどの方向にも向いていない場合に P^{v}_{ij}を小さくする用途のパラメータ
  5. Merged kernel P \in R^{N \times N}
    • P = (1 - \lambda) P^{v} + \lambda P^{s}
      • 論文では \lambda=0.2が安定した結果を出すと記載されている
      • カーネルの設定はユーザーに委ねられている*5。ベストプラクティスが特に無いので \lambda=0.2を使うしかなさそう。
  6. Macrostate identification
    • 単一細胞レベルのデータであるカーネル Pはノイズが大きいので、細胞集団(Macrostateと呼ぶ)レベルの情報へと変換する
    • GPCCA (Generalized Perron Cluster Cluster Analysis)
      1. カーネル PをSchur分解
        • P = QRQ^{T}
        • Q \in R^{N \times N}: ユニタリ行列 ( QQ^{*} = I) 各列がMacrostateに対応する基底ベクトル
        • R \in R^{N \times N}: Pの固有値 \lambda_{1}...\lambda_{l}が対角成分にある上三角行列
      2. 以下のいずれかの基準で上位のMacrostateを選ぶ
        • Eigengap heuristics (固有値に閾値を設ける方法) *6
        • minChi algorithm
        • Crispness
      3. 選ばれたMacrostateのみを含む基底ベクトル行列を \hat{Q} \in R^{N \times n_{s}}と呼ぶ
  7. Macrostate membership \chi \in R^{N \times n_{s}}
    • \chi = \hat{Q}A: \chi_{is}は細胞 iのState sとの類似度を表す
      • A: Rotation matrix *7
    • Aは以下の f_{n_{s}}(A)を最小化する最適化問題を解き求める
      • f_{n_{s}}(A) = n_{s} - \rm{trace}( \hat{D}^{-1} \chi^{T} D \chi)
      • \hat{Q}^{T} D Q = I
      • 制約条件
        • \chi_{is} \leq 0
        • \sum_{s} \chi_{is} = 1
      • これにより \chiの各列 (各Macrostateに該当する細胞のパターン) は直交に近づく
  8. Macrostate-level transition matrix P^{c} \in R^{n_{s} \times n_{s}}
    • P^{c} = ( \chi^{T} D \chi )^{-1} (\chi^{T} D P \chi)
  9. Terminal stateを推定する
    • 分化の終末にいるMacrostateは他の細胞への状態遷移が少ないと考えられる。したがってCellRankでは遷移行列 P^{c}の情報をもとに終末にあるMacrostateを以下のように定める。
    • State i is terminal if P^{c}_{ii} > \epsilon
      • \epsilon: Threshold (Default: 0.96)
  10. Initial stateを推定する
    1. Stationary distribution \pi \in R^{N}を求める
      • \pi: 定常状態にある細胞状態組成
      • \pi^{T}P = \pi^{T}
      • \sum_{i} \pi^{T}_{i} = 1
    2. \piをMacrostate-levelに変換
      • \pi_{p} = \chi^{T} \pi
    3. Initial state
      • 定常状態を「一定以上の時間が経過した後の細胞状態組成」と仮定すると、Initial stateの細胞は定常状態では少なくなると考えられる。したがってCellRankでは以下の基準で選択する。Initial stateの数 nはユーザーが決める必要がある。
      • State i is initial if \pi_{i} is in top n smallest values
  11. Terminal cells R_{t}を定義
    • Terminal state t ごとにMembership \chi_{t}の値が高い細胞をTerminal cells R_{t}とする
  12. 各細胞の運命を推定する
    • Transient cellとRecurrent cellという2つの状態を考える。Transient cellからはRecurrent cellへ遷移できるのに対し、反対の遷移は生じないとすると、Transition matrix Pは以下のように表せる
      • このとき A=(I - Q)^{-1}Sの A_{ij}がTransient cell iがRecurrent cellのうち jへ最初に到着する確率を表すことが証明されているらしい*8
    • CellRankではTerminal cell R_{t}をRecurrent cellと見なし、その他の細胞(Transient cell)への遷移をゼロに変換。上述の Aを求め、各細胞がどのTerminal stateへ辿り着くか (Absorption probabilityと呼んでいる)を推定する
 
P = \begin{bmatrix}
\hat{P}&0\\
S&Q
\end{bmatrix}

引用元：Lange et al. “ CellRank for directed single-cell fate mapping” bioRxiv 2020.10.19.345983; doi: https://doi.org/10.1101/2020.10.19.345983 CC-BY 4.0

*1:簡略化しているので詳細は論文を要参照

*2:σは

*3:ランダムウォークの際に終点で収束するように

*4:過去記事: https://auroratummy.hatenablog.com/entry/2021/12/07/011122

*5:https://cellrank.readthedocs.io/en/stable/kernels_and_estimators.html#Initialize-a-kernel

*6:https://cellrank.readthedocs.io/en/stable/kernels_and_estimators.html#Compute-a-matrix-decomposition

*7:前述のAdjacency matrixと違うので注意

*8:Tolverらの教科書が引用されていた。http://web.math.ku.dk/noter/filer/stoknoter.pdf

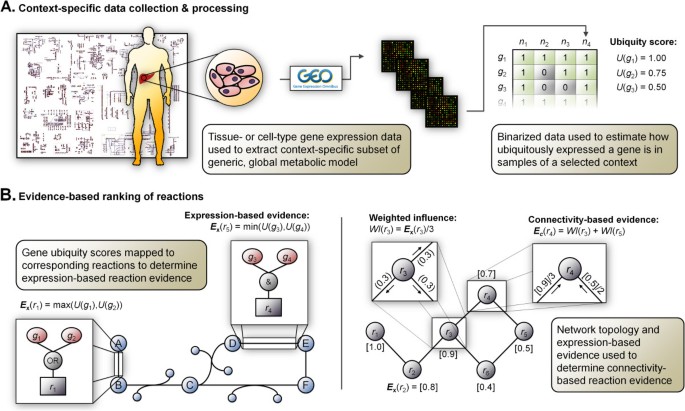
Context-specific metabolic modelingについて

Omics Bioinfo

Context-specific metabolic modeling

Context-specific metabolic modelingとは、トランスクリプトーム・プロテオーム等の発現情報を用いて、Recon3DやHuman1等の全代謝反応を含むGenome-scale metabolic model (GEMs)から、解析対象 (e.g. 特定の細胞、組織) で機能している・していない代謝反応のみを含むGEMsを抽出する手法。

2008年頃から色々な手法が提案されており、特に新しい研究分野ではないのだが、個人的なプロジェクトで似たような方法を試してみたいと考えている。ほとんどがMATLABで実装されていること (筆者はオープンソースで実装したい)、手法に応じて結果が大きく異なることが報告されていること *1 など、手法を理解していない状態で試すと危ない雰囲気なので、簡単にまとめてみようと思う。

Context-specific metabolic modelingの手法は以下のレビュー論文では3つのグループに分類されている。ここでは各グループの代表的な手法について調べる。

doi.org

GIMME-like family

上記論文では「発現量の低い遺伝子・タンパク質に対応する代謝反応の流束を最小化する」制約条件を利用した手法がGIMME-likeと分類されている。

GIMME

GIMMEは2008年にPalssonらによって発表された最初期の手法。(i) 遺伝子発現 (or タンパク発現) データ、(ii) 対象生物種のGEM、(iii) 発現の有無を決めるための閾値 (e.g. この閾値を上回る遺伝子は「発現あり」、下回る場合は「発現なし」とみなされる)、(iv) Required Metabolic Functionalities (RMF) (生物学的な知識に基づき存在していると考えられる代謝機能) を入力として受け取る。原著論文では「培地中の炭素源が生育につながる*2」ことをRMFとして設定している。

以下のステップで組織・細胞特異的なGEMsを構築する。

  1. 発現の無い (閾値を下回る) 遺伝子・タンパク質に対応する代謝反応をGEMから除外する
  2. RMFを実現できるように除外した代謝反応の一部を元に戻す
  3. RMFを最大化する代謝流束をFBAで推定する
  4. RMFがある値以上 (論文では3.で求めた最大値の0.9倍以上を基準としている) となる範囲で以下のInconsistency Score (IS) が最小となる代謝流束をFBAで計算する

Inconsistency scoreは下図のように設定されている。赤い矢印は対応する遺伝子の発現量が閾値 *3 を下回っている代謝反応を表す。最適な閾値を決める方法は本論文では特に提案されていない。閾値をいくつか試して結果への影響が小さかったことを確認している、とのこと。*4 上記のようにGIMME-like familyは遺伝子・タンパク質発現とある程度齟齬のない代謝流束で、Biomass functionなどの目的関数を最大化することを目指す手法である。

  • \sum_{i} c_{i} v_{i}: Inconsistency Score
  • v_{i}: 反応 iの流束
  • c_{i} = max(0, x_{cutoff} - x_{i})
    • x_{cutoff}: 閾値
    • x_{i}: 反応 iに対応する遺伝子の発現量

引用元：Becker SA, Palsson BO. Context-specific metabolic networks are consistent with experiments. PLoS Comput Biol. 2008 May 16;4(5):e1000082. doi: 10.1371/journal.pcbi.1000082. PMID: 18483554; PMCID: PMC2366062.

doi.org

iMAT-like family

上記レビュー論文では「低発現遺伝子に対応する代謝反応をできるだけ削り、高発現遺伝子に対応する代謝反応をできるだけ残す」最適化を行う手法をiMAT-likeと呼んでいた。GIMME-like familyは遺伝子発現データとの齟齬の少ない制約条件下でBiomass functionなどのRMFを最大化する代謝状態を探索する方法であったが、iMAT-like familyの手法はRMFを考慮せず、シンプルに遺伝子発現データとの齟齬の少ない代謝状態を探索する。

iMAT

iMATは2008年にShlomi・Palsson・Ruppinらによって提案された手法。(i) 遺伝子発現 (or タンパク発現) データ、(ii) 対象生物種のGEM、(iii) 発現レベルをHigh/Normal/Lowに分けるための閾値、(iv)パラメータ \epsilon (後述)を入力として受け取る。

以下の制約条件下で目的関数が最大となる代謝流束を見つける。この目的関数を最大化することで、高発現遺伝子に対応する代謝の流束ができるだけ非ゼロの値になり、低発現遺伝子に対応する代謝の流束がゼロになるような、遺伝子発現データとの齟齬の少ない代謝状態を探索できる。下記論文のFig. 1がイメージをつかみやすい*5。この問題はパラメータ yが整数値なので混合整数線形計画法 (MILP)で最適化を行う。MILPは線形計画法(LP)よりも最適解の探索が困難であるため*6、おそらくGIMMEなどのLPベースの手法よりも計算時間を要すると思われる。

  • 目的関数: \sum_{i \in R_{H}} (y_{i}^{+} + y_{i}^{-}) + \sum_{i \in R_{L}} \hat{y}_{i}^{+}
    • R_{H}: 高発現遺伝子に対応する代謝反応
    • R_{L}: 低発現遺伝子に対応する代謝反応
    • y_{i}^{+}: 代謝 iの順方向のFluxがある場合1、ない場合0のバイナリ変数
    • y_{i}^{-}: 代謝 iの逆方向のFluxがある場合1、ない場合0のバイナリ変数
    • \hat{y}_{i}^{+}: 代謝 iのFluxがある場合0、ない場合1のバイナリ変数
  • 制約条件
    1. Sv = 0 *7
    2. v_{min,i} \leq v_{i} \le v_{max,i} *8
    3. v_{i} + y_{i}^{+} (v_{min,i} - \epsilon) \geq v_{min, i}, i \in R_{H}
    4. v_{i} + y_{i}^{+} (v_{max,i} + \epsilon) \leq v_{max,i}, i \in R_{H}
      • \epsilon: このパラメータを設けることで、代謝が存在する ( y_{i}^{+} or y_{i}^{+}= 1の場合)にFluxがある程度の値になるように制約をかける
    5. v_{min,i}(1-\hat{y}_{i}^{+}) \leq v_{i} \leq v_{max,i}(1-\hat{y}_{i}^{+}), i \in R_{L}
    6. y_{i}^{+}, y_{i}^{-}, \hat{y}_{i}^{+} \in [0, 1]

www.nature.com

INIT (tINIT)

INITはJens Nielsenらのグループが2012年に発表した手法。その後2014年に改良版のtINITが発表された。INITは以下のように定式化されている。原著論文を読んでいてもわからない点があったのでレビューを参考にした。iMATと同様に一部のパラメータが整数値なのでMILPで最適化を行う。

  • 目的関数: \sum_{i \in R} w_{i} y_{i}
    • R: Reactions
    • M: Metabolites
    • w_{i}: 代謝反応 iのWeight
      • 代謝反応 iに対応する遺伝子・タンパクの発現レベルに応じて値を変える
      • 2012年のオリジナル論文では w_{i} = 5log(\frac{Average_{i}}{Signal_{i,j}})としている *9
  • 制約条件
    • Sv = b: INITは定常状態を仮定しない
      • b_{j} \geq \sigma, j \in KeyMet: 代謝物 jが対象細胞・組織に存在することが知られている場合は \sigma *10 以上物質産生が起こっていると仮定 *11
      • b_{j} = 0, j \notin KeyMet
    • y_{i} \in [0,1]: 代謝反応 i が存在する場合は1、除外された場合は0
    • y_{i} v_{min,i} \leq v_{i} \leq y_{i} v_{max,i}

引用元：Agren R, Bordel S et al. Reconstruction of genome-scale active metabolic networks for 69 human cell types and 16 cancer types using INIT. PLoS Comput Biol. 2012;8(5):e1002518. doi: 10.1371/journal.pcbi.1002518. Epub 2012 May 17. PMID: 22615553; PMCID: PMC3355067.

journals.plos.org

https://www.embopress.org/doi/full/10.1002/msb.145122www.embopress.org

MBA-like family

遺伝子発現データを元にGEMから発現の無い枝を取り除く(Pruning)する手法。この手法はGIMME-like familyやiMAT-like familyのように特定の代謝状態を探索するのではなく、

MBA

MBAは2010年にJerby・Shlomi・Ruppinによって提案された手法。下記の目的関数を最大化するPartial model (PM)を以下のアルゴリズムで探索する*12。Globam model (GM) から少しずつ不必要な反応を削っていくアプローチである。2. でCore reactions ( C_{H}, C_{M}) に含まれない反応の集合 Pを抽出。3.以降のFor loopでは、 Pに含まれる反応 rを一つずつKOして、その結果Inactiveになる反応を除外する (枝葉を切る, pruning)。CheckModelConsistencyはモデル R_{P}から反応 rを除外したときにInactiveになる反応を返す関数。

2.において Pに含まれる反応 rの順番はランダムに決める。反応 rの並びによって最終的なGEMの形が変わるので、論文ではpruningを1000回行い、できた1000個のGEMから共通性の高い領域を抽出している。

  • 目的関数: |R_{P} \cap C_{M}| - \epsilon | R_{P} \setminus (C_{M} \cup C_{H})|
    • Core reactions: C
      • C_{H}: 高確率で存在する代謝反応 (e.g. 文献・実験由来の情報)
      • C_{M}: 中確率で存在する代謝反応 (e.g. オミクス由来の情報)
    • Global model: GM = (M_{G}, R_{G}, S_{G}, L_{G})
      • M: 代謝物
      • R: 代謝反応
      • S: Stoichiometry matrix
      • L: Limitation of flux (各流束の最大・最小値)
    • Partial model: PM = (M_{P}, R_{P}, S_{P}, L_{P})
      • C_{H} \in R_{P}: PMは C_{H}の全反応を含む

アルゴリズム

f:id:auroratummy:20220118002936p:plain 引用元：Jerby, Livnat et al. “Computational reconstruction of tissue-specific metabolic models: application to human liver metabolism.” Molecular systems biology vol. 6 (2010): 401. doi:10.1038/msb.2010.56

www.ncbi.nlm.nih.gov

mCADRE

mCADREはMBAを改良した方法で2012年に発表された。MBAがFor loopのiterationの順番をランダムに決めていたことを問題視。近傍にCore reactionがあるかを考慮したスコアを設定し、Non-core reaction Pに含まれる反応を並べることで、一意な結果が得られる(かつMBA論文のように1000回 iterationを実施する必要がないのでより短い時間で計算できる)手法を提案。

引用元：Wang, Y., Eddy, J.A. & Price, N.D. Reconstruction of genome-scale metabolic models for 126 human tissues using mCADRE. BMC Syst Biol 6, 153 (2012). https://doi.org/10.1186/1752-0509-6-153

bmcsystbiol.biomedcentral.com

Pythonで上記の手法を試すには

Pythonでは以下のライブラリに各手法が実装されている。Context-specific modelingの関数・クラスについての説明がほとんど存在しないツールもあるので、本当に使えるのか？だが、実装する際に参考になると思われる。

*1:https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1006867

*2:Biomass産生につながる

*3:この論文の場合は12.0

*4:Data not shownだが

*5:著作権の関係で引用できない

*6:https://www.msi.co.jp/nuopt/introduction/algorithm/mip.html

*7:一般的なFVAの制約条件：定常状態

*8:これも一般的なFVAの制約条件：事前情報に基づく各代謝の最大・最小流束

*9:Tissue jにおける発現値を全Tissueの平均値と比較

*10:small positive value

*11:これによってこの物質の産生に関わる代謝反応が除外されることを防ぐ

*12:なぜかこの論文では差集合をバックスラッシュでなくスラッシュで表しているので注意

マイクロバイオーム解析④：COBRApyで細菌の代謝をモデリングする（２）

Bioinfo Microbiome

2細菌が同じ環境にいるときの代謝を推定する

前回の記事の続き。2種類の細菌が同じ環境にいるときに、Cooperative/Competitiveな関係になるのか、どのように代謝物を交換するのか、といった細菌間相互作用をCOBRApyを使ったFBA (Flux Balance Analysis)で推定してみる。

ここでは以下の論文のFig. 4dで示されているように、Bacteroides caccae ATCC 43185とLactobacillus rhamnosus GGをDMEM 6429という培地で共培養した場合の細菌間相互作用を推定してみる。

www.nature.com

本記事の検証に使ったコードはgithubにアップした。

github.com

２生物種のGEMsを作る方法

この論文ではBacteroides caccae ATCC 43185とLactobacillus rhamnosus GGのGEMs (Genome-scale metabolic models) を連結させた代謝モデルを作り、両細菌の生育率の合計が最大になる場合の代謝流束をFBAで求めている。メソッドを読むと筆者らが2015年の論文に用いた細菌間に共通する区画*1を設ける手法を利用していた。この手法のオリジナルは以下の2010年の論文のようだ。このオリジナル論文のFig. 2が仕様を理解する上でわかりやすかった。

doi.org

引用元：Kitgord and Segre. PLoS Comput Biol. 2010 Nov 18;6(11):e1001002. doi: 10.1371/journal.pcbi.1001002.

Fig. ABは各細菌のGEMsである。区画CYT1とCYT2は各細菌の細胞内領域、EX1とEX2は各細菌の細胞外領域、X・Y・Zは代謝物質を表す。この手法ではFig. Cのように２つのGEMsに追加して、細菌間で共通の区画ENVを設定する。

これはStoichiometric matrixで表すとFig. EFGのように表せる。各細菌のStoichiometric matrix (Fig. EF) に若干手を加えるだけで２種共培養のStoichiometric matrix (Fig. G) を作ることができる。

MATLAB版のCOBRAには2細菌のモデルを作るための機能が用意されているが*2、COBRApyでは見当たらない。すでにMMINTEというライブラリが同様の機能をPythonで実装しているようなので、それを使ってみる。

doi.org

MMINTEのgithubページにおいてあったスクリプトを参考に以下のコードを走らせるとエラーが出た。

import mminte
species = ["Bacteroides_caccae_ATCC_43185", "Lactobacillus_rhamnosus_GG_ATCC_53103"]
model_filenames = ["AGORA/CurrentVersion/AGORA_1_03/AGORA_1_03_sbml/{s}.xml".format(s=s) for s in species]
pairs = mminte.get_all_pairs(model_filenames)
pair_model_filenames = mminte.create_interaction_models(pairs, ".")
pair_model_filenames

RuntimeError: The heuristic for discovering an external compartment relies on names and boundary reactions. Yet, there are neither compartments with recognized names nor boundary reactions in the model.

エラーメッセージを見ても原因がよくわからなかったので、MMINTEのコードをチェックしてみた。上記の関数mminte.create_interaction_modelsの中では関数create_community_modelが主要な働きをしている様子。

import six
community_compartment = "u" # lumen

# MetaboliteのSuffixをチェックする
#   e.g. ****[e] はExtracellular metaboliteを表すbigg形式のSuffix
modelseed_suffix_re = re.compile(r'_([ce])$')
bigg_suffix_re = re.compile(r'\[([cepu])\]$')
def _id_type(object_id):
    if re.search(bigg_suffix_re, object_id) is not None:
        return 'bigg'
    if re.search(modelseed_suffix_re, object_id) is not None:
        return 'modelseed'
    return 'unknown'

# Metaboliteの場所 (Compartment) を変更する関数
def _change_compartment(id_str, compartment, id_type):
    if id_type == 'bigg':
        return re.sub(bigg_suffix_re, '[{0}]'.format(compartment), id_str)
    elif id_type == 'modelseed':
        return re.sub(modelseed_suffix_re, '_{0}'.format(compartment), id_str)
    return '{0}_{1}'.format(id_str, compartment)


def create_community_model(model_files, model_names):
    # 空のGEMsを作成する
    community = cobra.Model('Community')

    # Exchange reaction IDのリスト (後に重複しないようにリストを作成する)
    exchange_reaction_ids = set()

    # 各生物のGEMsを追加する
    for model_file, model_name in zip(model_files, model_names):
        # GEMの読み込み
        model = cobra.io.read_sbml_model(model_file)

        # 
        linear_coefficients = cobra.util.solver.linear_reaction_coefficients(model)
        objective_id = '{0}_{1}'.format(model_name, six.next(six.iterkeys(linear_coefficients)).id)
        objective_value = six.next(six.itervalues(linear_coefficients))

        # 各MetaboliteのCompartmentの情報が存在するかMetabolite IDのSuffixをもとに確認
        for metabolite in model.metabolites: metabolite.notes['type'] = _id_type(metabolite.id)
        unknown = model.metabolites.query(lambda x: 'unknown' in x['type'], 'notes')
        if len(unknown) > 0:
            raise Exception('Unknown compartment suffixes found in metabolites for {0}'.format(model_file))

        # 各細菌のGEMsのExchange reactionのリストを取得する
        exchange_reactions = model.exchanges

        # 細菌間で共通の区画`ENV`を設定する
        for reaction in exchange_reactions:
            if reaction.id not in exchange_reaction_ids:
                exchange_reaction_ids.add(reaction.id)
                metabolite = six.next(six.iterkeys(reaction.metabolites)).copy()
                # MetaboliteのCompartmentを"e"からlumen ("u")へ変更
                metabolite.compartment = community_compartment
                metabolite.id = _change_compartment(metabolite.id, community_compartment, metabolite.notes['type'])
                community.add_metabolites(metabolite)
                rxn = community.add_boundary(metabolite)  # This is slow on cobra06
                rxn.id = reaction.id  # Keep same ID as species model

        for reaction in model.reactions:
            if reaction in exchange_reactions:
                # 区画`ENV`と`EX`の間の物質交換を定義する
                e_metabolite = six.next(six.iterkeys(reaction.metabolites))
                u_metabolite = community.metabolites.get_by_id(
                    _change_compartment(e_metabolite.id, community_compartment, e_metabolite.notes['type']))
                reaction.add_metabolites({u_metabolite: 1.})
                # Reaction ID の名前を変える (各細菌の反応を区別するため)
                reaction.id = '{0}_TR_{1}'.format(model_name, reaction.id[3:]) # Strip "EX_" prefix
                reaction.bounds = (-1000., 1000.)
            else:
                # Reaction ID の名前を変える (各細菌の反応を区別するため)
                reaction.id = '{0}_{1}'.format(model_name, reaction.id)

        # Metabolite ID の名前を変える (各細菌の物質を区別するため)
        for metabolite in model.metabolites:
            if metabolite.compartment != community_compartment:
                metabolite.id = '{0}_{1}'.format(model_name, metabolite.id)

        # あたらしいGEMに追加する
        community += model

        # 各細菌のBiomass functionを目的関数に追加
        objective_reaction = community.reactions.get_by_id(objective_id)
        cobra.util.solver.set_objective(community, {objective_reaction: objective_value}, additive=True)
    
    # GEMに名前をつける
    community.id = 'x'.join(model_names)

    return community

cobra.Model.add_metabolitesで上記のエラーメッセージが出ていた。調べると以下のメソッドが関わっていそうなことがわかった。cobra.Model.compartments == "u"が細胞外を表す区画だと認識されていないようだ。おそらくMMINTEが開発された頃からCOBRAの仕様が変わったものと思われる。

import logging
LOGGER = logging.getLogger(__name__)

# cobra.Model.compartmentsから細胞外のCompartmentを見つける
def find_external_compartment(model):
    if model.boundary:
        counts = pd.Series(tuple(r.compartments)[0] for r in model.boundary)
        most = counts.value_counts()
        most = most.index[most == most.max()].to_series()
    else:
        most = None
    like_external = cobra.medium.annotations.compartment_shortlist["e"] + ["e"]
    matches = pd.Series(
        [co in like_external for co in model.compartments], index=model.compartments
    )

    if matches.sum() == 1:
        compartment = matches.index[matches][0]
        LOGGER.info(
            "Compartment `%s` sounds like an external compartment. "
            "Using this one without counting boundary reactions" % compartment
        )
        return compartment
    elif most is not None and matches.sum() > 1 and matches[most].sum() == 1:
        compartment = most[matches[most]][0]
        LOGGER.warning(
            "There are several compartments that look like an "
            "external compartment but `%s` has the most boundary "
            "reactions, so using that as the external "
            "compartment." % compartment
        )
        return compartment
    elif matches.sum() > 1:
        raise RuntimeError(
            "There are several compartments (%s) that look "
            "like external compartments but we can't tell "
            "which one to use. Consider renaming your "
            "compartments please."
        )

    if most is not None:
        return most[0]
        LOGGER.warning(
            "Could not identify an external compartment by name and"
            " choosing one with the most boundary reactions. That "
            "might be complete nonsense or change suddenly. "
            "Consider renaming your compartments using "
            "`Model.compartments` to fix this."
        )
    # No info in the model, so give up
    raise RuntimeError(
        "The heuristic for discovering an external compartment "
        "relies on names and boundary reactions. Yet, there "
        "are neither compartments with recognized names nor "
        "boundary reactions in the model."
    )

cobra.Model.copartmentsが以下のどれかだと、外部環境を表す区画として認識してくれる様子。

cobra.medium.annotations.compartment_shortlist["e"] + ["e"]

['extracellular',
 'extraorganism',
 'out',
 'extracellular space',
 'extra organism',
 'extra cellular',
 'extra-organism',
 'external',
 'external medium',
 'e']

community_compartment = "out"としたら問題なく走るようになった。

結果

species = ["Bacteroides_caccae_ATCC_43185", "Lactobacillus_rhamnosus_GG_ATCC_53103"]
model_filenames = ["AGORA/CurrentVersion/AGORA_1_03/AGORA_1_03_sbml/{s}.xml".format(s=s) for s in species]

# 共培養GEMをつくる
community = create_community_model(model_filenames, species)

# Mediumの設定：Arabinogalactoseを除外した場合
medium = community.medium
for k in medium.keys(): medium[k] = 0
for ex,val in zip(dmem["Exchange reaction ID"], dmem["Uptake rate"]):
    if community.reactions.has_id(ex): medium[ex] = val
medium["EX_ala_L(e)"] = 0
medium["EX_arabinogal(e)"] = 0
community.medium = medium
op = community.optimize()
print("DMEM with Vitamin K, Hemin: {g}".format(g=op.objective_value))
print("  {s}: {g}".format(s=community.notes["species"][0]["name"], g=op.fluxes[community.notes["species"][0]["objective"]]))
print("  {s}: {g}".format(s=community.notes["species"][1]["name"], g=op.fluxes[community.notes["species"][1]["objective"]]))

# Mediumの設定：Arabinogalactoseありの場合
medium = community.medium
for k in medium.keys(): medium[k] = 0
dmem = pd.read_table("Magnusdottir-2017-Nat_Biotechnol/Medium-DMEM_6429.tsv")
for ex,val in zip(dmem["Exchange reaction ID"], dmem["Uptake rate"]):
    if community.reactions.has_id(ex): medium[ex] = val
medium["EX_ala_L(e)"] = 0
community.medium = medium
op = community.optimize()
print("DMEM with Vitamin K, Hemin, Arabinogalactan: {g}".format(g=op.objective_value))
print("  {s}: {g}".format(s=community.notes["species"][0]["name"], g=op.fluxes[community.notes["species"][0]["objective"]]))
print("  {s}: {g}".format(s=community.notes["species"][1]["name"], g=op.fluxes[community.notes["species"][1]["objective"]]))

各細菌の生育率は以下のように推定された。Lactobacillus rhamnosus GG単独のGEMにFBAを適用すると、Arabinogalactanが無いとDMEM培地では生育しないと推定されたが*3、共培養するとArabinogalactanなしでも生育すると推定された。

  • Arabinogalactose あり
    • Bacteroides_caccae_ATCC_43185: 0.4386544423746743
    • Lactobacillus_rhamnosus_GG_ATCC_53103: 0.22080916149500934
  • Arabinogalactose なし
    • Bacteroides_caccae_ATCC_43185: 0.24543405369998675
    • Lactobacillus_rhamnosus_GG_ATCC_53103: 0.11140717070316093

*1:論文ではlumenと呼んでいる

*2:https://opencobra.github.io/cobratoolbox/latest/tutorials/tutorialMicrobeMicrobeInteractions.html

*3:論文と同じ＆前回記事参照